Active matter

Bose-Einstein-like condensation transition for scalar active matter

Collaborators: Ramin Golestanian, Benoît Mahault, Aritra Bose (Max Planck Institute for Dynamics and Self-Organisation, Germany)

One example of an exotic phenomenon that can occur in active matter systems is the emergence of a Bose-Einstein like condensation transition for scalar active matter, where multiple particles can occupy the same energy level. Due to the presence of a diffusivity edge where the diffusion coefficient drops non-smoothly to zero, the particles in the condensate lose the ability to move and are effectively “frozen” is that state. My research investigates the steady-state properties of such systems under the influence of an external driving force, which can modify the condensation transition drastically, even allowing for the existence of a low-temperature ‘evaporation’ transition, making the condensation a reentrant phenomenon [1]. Studying the full dynamics of such systems instead of only the steady state can also lead to finite-time condensation transitions, which can be tuned by judiciously choosing a confining potential [2].

Non-Gaussian anomalous dynamics in systems of interacting run-and-tumble particles

In contrast with regular Brownian motion, where a particle’s position follows a Gaussian distribution, in complex environments like living cells and crowded fluids, non-Gaussian anomalous dynamics occur, deviating from Gaussian behavior.While most research focuses on equilibrium systems, understanding the motion of particles in non-equilibrium systems is challenging due to the lack of a complete theory of non-equilibrium statistical mechanics. Recent progress has been made in studying simple non-equilibrium systems, including low-dimensional exclusion processes and active matter.

In this context, my research investigates the motion of a tagged particle in different models: a bead-spring polymer model and a lattice model of run-and-tumble particles [3]. The results reveal various regimes of motion, including ballistic, superdiffusive, subdiffusive, and diffusive behavior. The lattice model exhibits atypical, non-Gaussian dynamics due to a dynamically changing environment for the tagged particle. For this model, the position PDF can be approximately described by a Laplacian distribution, a particular choice that is also found in experiments on, e.g., the displacement of RNA-protein particles in E. Coli. The basic physical idea is that the diffusivity $D$ of a particle diffusing in a complex medium evolves in time due to the heterogeneities of the environment. This is described by a time dependent diffusivity $D(t)$ that also evolves stochastically, by means of a superstatistical approach.

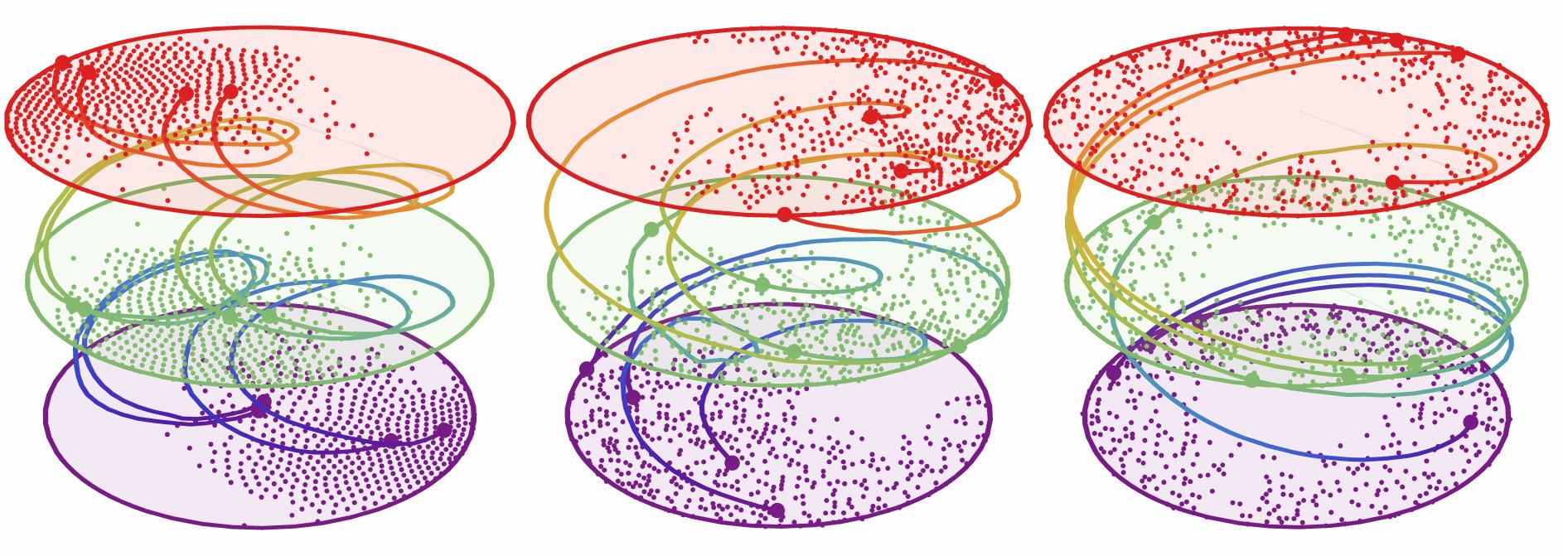
Chaotic mixing for confined active matter

For many lab-on-a-chip applications in modern medicine, the study of mixing in microfluidics is of seminal importance. However, due to high Peclet and low Reynolds numbers, both diffusion and turbulence are ineffective approaches to induce efficient mixing. The only remaining avenue is then active stirring, which needs to be fine-tuned to result in chaotic mixing. My research investigates whether active particles in confined geometries (such as a microfluidic sensor) can act as active stirrers, removing the need for mechanical stirring or the microscale attunement of the boundary in order to generate chaotic mixing. Since the particles trace out entangled spacetime trajectories, I use braiding theory to find the optimal parameter configurations leading to the highest degree of mixing.

References:

[1] Jonas Berx, Aritra Bose, Ramin Golestanian and Benoît Mahault, "Reentrant condensation transition in a model of driven scalar active matter with diffusivity edge", EPL 142, 67004 (2023)

[2] Jonas Berx, "Dynamic control of the Bose-Einstein-like condensation transition in scalar active matter", under review in New Journal of Physics (2024)

[3] Stefanie Put, Jonas Berx and Carlo Vanderzande, "Non-Gaussian anomalous dynamics in systems of interacting run-and-tumble particles", J. Stat. Mech., 2019(12), 123205 (2019)