Hierarchical deposition

Collaborators: Joseph Indekeu (KU Leuven, Belgium)

Hierarchical random deposition

Traditionally, general deposition models (e.g., random solid-on-solid, ballistic deposition, etc.) assume that all particles are identical in every aspect and that deposition occurs sequentially. The hierarchical random deposition model (HRDM) deviates from the assumptions of these models by considering synchronous deposition [1]. This means that particles of the same size are all deposited simultaneously in “generations.” This synchronous deposition is governed by a power law based on the size of the particles. The HDM is particularly useful for studying systems with power-law particle distributions, as observed in, e.g., pyroclastic clouds originating from volcanic eruptions, asteroid fragmentation, and laboratory experiments involving multifragmentation.

The number of particles of linear size $s$ is denoted by $N(s)$ and follows a scaling relationship $N(s) = \lambda^{-1} N(s/\lambda)$, where the number of particles is proportional to the inverse impact cross-section. The resulting landscape exhibits a logarithmic fractal law for its surface or length. Initially, the unit interval is divided into subsets of length $1/\lambda$. Each subset is either populated with a particle “hill” with probability $P$ or a “hole” with probability $Q$, which reduces the height by a factor $\lambda$. The third option is to do nothing with probability $1 - S$. This process can be continued ad infinitum.

My research aims to uncover the connection between coastal point/coastline formation and the percolation properties of the HRDM. It can be shown that when the system undergoes a percolation transition, the number of coastal points transitions from a fractal behaviour to a Euclidean one. Exactly at the percolation transition probability $P_c$, the number of coastal points increases linearly with the generation $n$, exhibiting a logarithmic fractal behaviour.

Visibility networks

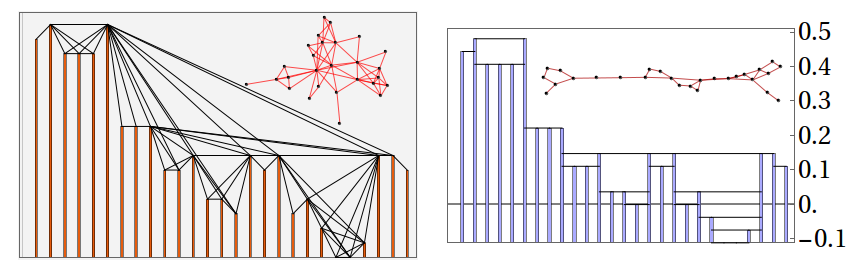
To map linear data such as time series or surface topology to complex networks, a Visibility Algorithm (VA) can be used. The essence of such a VA lies in creating a network representation by assigning nodes to each data point and establishing edges based on the mutual visibility between them. The algorithm determines whether a line of visibility between two data points is “intersected” by any intermediate data, and if not, it assigns an edge between them.

There are two main types of the VA: the Natural Visibility Algorithm (NVA) and the Horizontal Visibility Algorithm (HVA). The NVA considers the visibility line as a direct connection between two data points and includes inclination with respect to a chosen baseline. In contrast, the HVA focuses on mutual horizontal visibility between data points and disregards inclination with respect to the baseline. The graph generated by the HVA is always a subgraph of the NVA, as horizontal visibility implies natural visibility between two data points.

My research analyses the HRDM by mapping it to a scale-free network by means of the HVA. The resulting network can be shown to be fractal, self-similar, and exhibits hierarchical clustering.

References:

[1] Jonas Berx, Evi Bervoets, Claudiu V. Giuraniuc and Joseph O. Indekeu, "Coastlines and percolation in a model for hierarchical random deposition", Physica A 574, 125998 (2021)

[2] Jonas Berx, "Hierarchical deposition and scale-free networks: A visibility algorithm approach", Phys. Rev. E 106, 064305 (2022)