Stochastic Thermodynamics

Collaborators: Karel Proesmans (Niels Bohr International Academy, Denmark)

Stochastic thermodynamics provides a framework for understanding and quantifying the thermodynamic behaviour of small-scale systems that deviate from equilibrium, taking into account the effects of fluctuations and noise. In contrast with equilibrium thermodynamics, work and heat are treated as random variables in stochastic thermodynamics, where they can be determined on the level of single trajectories.

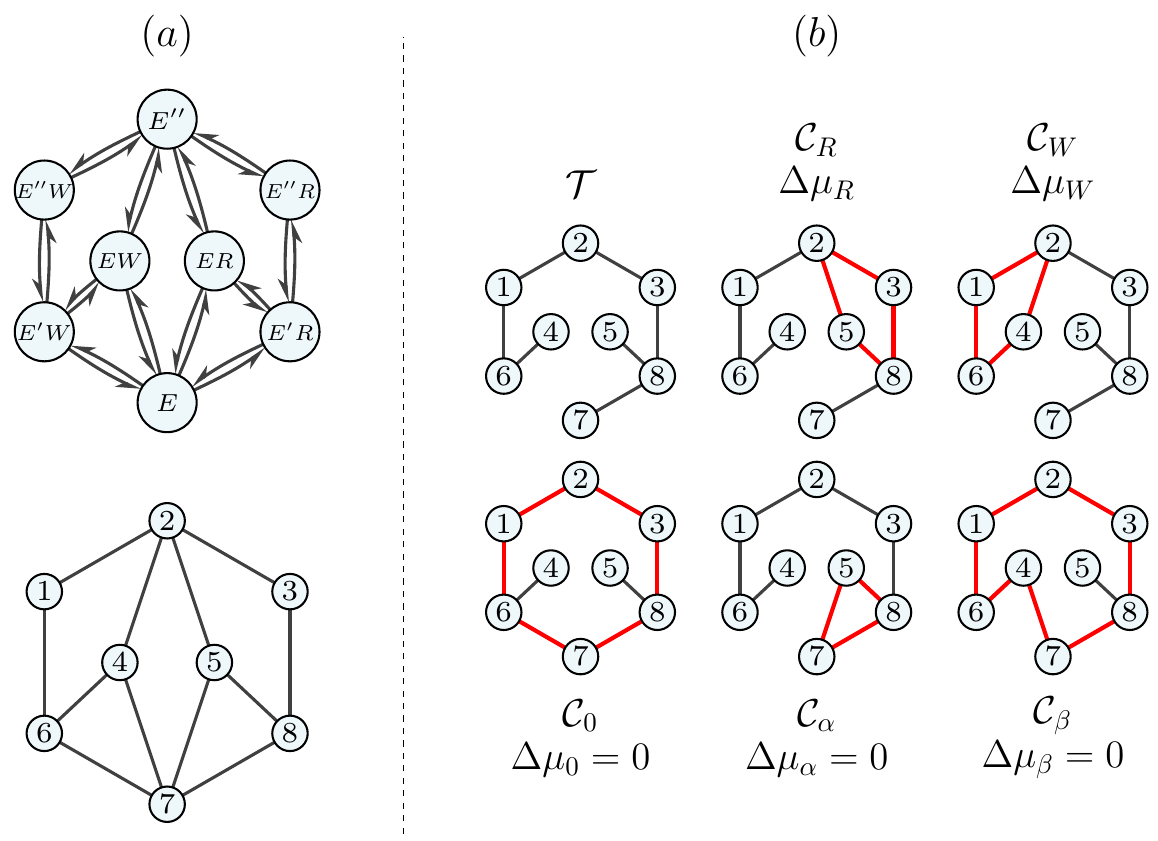
My research focuses on the stochastic behaviour of chemical reaction networks involved in (biochemical) replication processes. The most well-known of these is kinetic proofreading (KPR), where energy can be consumed, e.g., in the form of ATP hydrolysis, in order to increase accuracy on a microscopic scale. More specifically, I look at a form of proofreading called “energy relay proofreading”, which is able to increase the accuracy without consuming ATP molecules by making use of the energy released through catalysis to elevate the enzyme to a higher energy state, from which it can then irreversibly proofread. Below, I show an example of a proofreading scheme that makes use of an energy relay to differentiate between right ($R$) and wrong ($W$) substrates. There exist thermodynamic bounds on the precision of any fluctuating quantity, e.g., the correct substrate production current $\mathcal{J}_R$, where the thermodynamic uncertainty relation (TUR) tells us that in order to increase precision, the dissipation rate increases. In other words: precision always comes at a price. It is generally expressed as follows:

\[\mathcal{Q}\equiv T\sigma t\epsilon^2 \geq 2 k_B T\,,\]

where $T$ is the temperature, $\sigma$ is the entropy production rate, $\epsilon^2 = Var(\mathcal{J}_R)/\langle X\rangle^2$ is the precision, $t$ is the observation time and $k_B$ is the Boltzmann constant.

This project has received funding from the European Union’s Horizon Europe research and innovation programme under grant agreement No. 101104602